Calculation of Symmetrical Components

We are now aware of the concept of Sequence components of current / voltage. If you have miss this concept, please read Concept of Symmetrical Components.

Now we are at a stage to calculate the zero, positive and negative sequence components of current / voltage. As already discussed any three phase unbalanced voltage / current can be resolved into three set of balanced vectors. Thus we will use this concept to calculate the positive, negative and zero sequence components of voltages. Mind that the same philosophy is applicable for current also.

Before going into the calculation part, let us introduce ourselves with an operator ?. ? is an operator which when multiplied to any vector quantity, rotates the vector by an angle of 120� in anticlock wise direction without changing the magnitude of the vector. This means that ? must have a magnitude unity. From this definition we can write ? as below.

? = e^i2p/3

   = Cos(2p/3) + jSin(2p/3)

   = -0.5 + j0.866

Why not to explore more properties of ?? Sure, we must�

?² = e^i4p/3

   = Cos(4p/3) + jSin(4p/3)

   = Cos(2p - 2p/3) + jSin(2p - 2p/3)

   = Cos(2p/3) - jSin(2p/3)

   = -0.5 - j0.866

and

?³ = e^i6p/3= e^i2p

    = Cos(2p) + jSin(2p)

    = 1

? ?³� 1 = 0

? (? + 1)(1 + ?² + ?) = 0

As (? + 1) cannot be zero, therefore

1 + ?² + ? = 0

Thus to summarize the properties of operator ?,

?³= 1

?⁴= ?³. ? = ?

1 + ?² + ? = 0

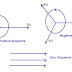
Consider the figure below where a three phase unbalanced voltages V_a, V_band V_c are resolved into three set of balanced voltages.

According to the Concept of Symmetrical components,

V_a = V_a1+ V_a2 + V_a0  �������(1)

V_b = V_b1+ V_b2 + V_b0 �������.(2)

V_c = V_c1+ V_c2 + V_c0 �������..(3)

But taking V_a1 reference and applying the concept of operator ?,

V_b1 = ?²V_a1

V_c1 = ?V_a1

Similarly for Negative Sequence we can write as

V_b2 = ?V_a2

V_c2 = ?²V_a2

Fortunately for Zero Sequence,

V_a0 = V_b0= V_c0

Thus from equation (2) and (3),

V_b = ?²V_a1+ ?V_a2 + V_b0  ������(4)

V_c = ?V_a1+ ?²V_a2 + V_c0  ������.(5)

Now, multiplying equation (4) by ? and (5) by ?² and adding them to equation (1), we get

V_a + ?V_b+ ?²V_c

= V_a1(1+ ?³+ ?³) + V_a2(1+ ?²+ ?⁴) + V_a0(1+ ? + ?²)

= 3V_a1 + V_a2(1+ ? + ?²)

= 3V_a1

? V_a1 = (V_a+ ?V_b + ?²V_c ) / 3  �������(6)

For getting negative sequence component, multiply equation (4) by ?² and (5) by ? & add them to equation (1),

V_a + ?²V_b+ ?V_c

= V_a1(1+ ?⁴+ ?²) + V_a2(1+ ?³+ ?³) + V_a0(1+ ? + ?²)

= 3V_a2

? V_a2 = (V_a+ ?²V_b + ?V_c) / 3  ��������(7)

For Zero Sequence component, add equation (1), (4) and (5),

V_a + V_b+ V_c

= V_a1(1+ ?+ ?²) + V_a2(1+ ?+ ?²) + 3V_a0

= 3V_a0

? V_a0 = (V_a+ V_b + V_c) / 3  ��������(8)

Therefore from equation (6), (7) and (8), we have completely calculated the positive, negative and zero sequence voltages.

In the same way, we can calculate the three components of currents. For currents we can write as below.

I_a1= (I_a + ?I_b + ?²I_c ) / 3 

I_a2= (I_a + ?²I_b + ?I_c) / 3 

I_a0= (I_a + I_b + I_c) / 3